• We will analyze trigonometric identities numerically and graphically • We will discuss techniques used to manipulate and simplify expressions in order to prove trigonometric identities algebraically Recall A trigonometric identity is an equation formed by the equivalence of two trigonometric expressions🎉 Meet students and ask top educators your questions Join Here!Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics trigonometricequationcalculator Tan^{2} en Related Symbolab blog posts I know what you did last summer

Trigonometric Identities
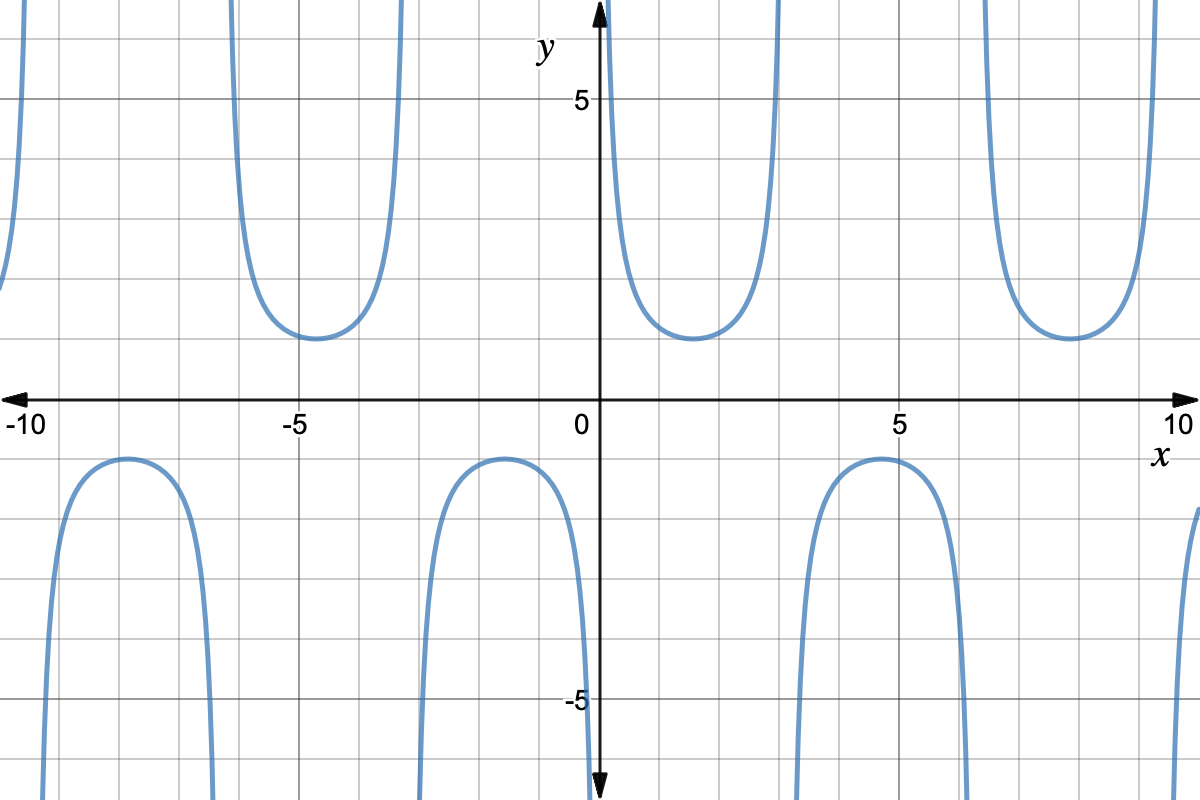
Trigonometric identities tan^2
Trigonometric identities tan^2-Rd Sharma Solutions for Class 10 Math Chapter 11 Trigonometric Identities are provided here with simple stepbystep explanations These solutions for Trigonometric Identities are extremely popular among Class 10 students for Math Trigonometric Identities Solutions come handy for quickly completing your homework and preparing for exams Trigonometric Identities The distances or heights can be calculated using mathematical techniques that fall under the category of 'trigonometry'The word 'trigonometry' comes from the Greek words 'tri' (meaning three), 'gon' (meaning sides), and 'metron' (meaning measure) (meaning measure)




Which Of The Following Are Trigonometric Identitie Gauthmath
Cos θ = 1/Sec θ or Sec θ = 1/Cos θ;Even Odd Identities sin − ˙=−sin csc − ˙=−csc cos − ˙=cos sec − ˙=sec tan − ˙=−tan cot − ˙=−cot Comple x Numbers Expansions 230 =cos ?Tables show common trigonometric identities and formulas such as Pythagorean trigonometric identity, sine of half angle formula, etc > Mathematical tables trigonometry identities formulas Home Blog FAQ About New Calculla About us Contact Show source t a n (2 α) = 2 t a n (α) 1 − t a n 2 (α) tan(2 \alpha) = \frac{2 tan
We will apply the following more fundamental trigonometric identity $\boxed{\tan^2 x 1 = \sec^2 x}$ The proof is started from the righthand side In the first method, we used the identity \({\sec}^2 \theta={\tan}^2 \theta1\) and continued to simplify In the second method, we split the fraction, putting both terms in the numerator over the common denominator This problem illustrates that there are multiple ways we can verify an identityIdentities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tan x equation 5 sin 2 x cos 2 x = 1 equation 6 tan 2 x 1 = sec 2 x equation 7 1 cot 2 x = csc 2 x equation 8 cos (x y) = cos x cos y sin x sin y equation 9 sin (x y) = sin x cos y cos x sin y equation 10 cos (x) = cos x equation 11
Tan θ = 1/Cot θ or Cot θ = 1/Tan θ;Trigonometric identities Prove that \tan ^{2} \theta1=\sec ^{2} \theta Our Discord hit 10K members!TRIGONOMETRIC IDENTITIES By Joanna GuttLehr, Pinnacle Learning Lab, last updated 5/08 Pythagorean Identities sin (A) cos (A) 1 1 tan (A) sec (A) 1 cot (A) csc2 (A)Quotient Identities sin( )
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



3
Trigonometry Identities Quotient Identities tan𝜃=sin𝜃 cos𝜃 cot𝜃=cos𝜃 sin𝜃 Reciprocal Identities csc𝜃= 1 sin𝜃 sec𝜃= 1 cos𝜃 cot𝜃= 1 tan𝜃 Pythagorean Identities sin2𝜃cos2𝜃=1 tan 2𝜃1=sec2𝜃 1cot2𝜃=csc2𝜃 Sum & Difference Identities sin( )=sin cos cos sin Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube 3 W H E R E I S T A N 1 Zonealarm Results Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un LivreTrig Equations and Identities wwwnaikermathscom 4 (a) Given that sin q = 5 cos q, find the value of tan q(1) (b) Hence, or otherwise, find the values of q in the interval 0 £ q < 360° for which sin q = 5 cos q, giving your answers to 1 decimal place (3) June 06 Q6



Http College Cengage Com Mathematics Larson Trigonometry 6e Instructors Downloads Instr Trig6 S21 Pdf




The Other Trigonometric Functions Precalculus Ii
Prove the following trigonometric identities (1tan^2 θ)(1sinθ)(1sinθ) = 1 asked May 15 in Trigonometry by Gaatrika ( 319k points) trigonometric identitiesA trigonometric identity is an equation containing trigonometric ratios of an angle that is true for all values of the angle(s) involved Fundamental identities of trigonometry (1) \(\sin^2 \theta \cos^2 \theta = 1\)Trigonometric identities Prove that \tan ^{2} \theta1=\sec ^{2} \theta 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨 Claim your spot here Books




Check My Work Evaluating Tan Frac 7 Pi 8 Using A Half Angle Formula Mathematics Stack Exchange




Trigonometry Choice Board Trigonometric Functions Trigonometry
The Pythagorean identities are based on the properties of a right triangle cos2θsin2θ =1 1tan2θ =sec2θ 1cot2θ =csc2θ cos 2 θ sin 2 θ = 1 1 tan 2 θ = sec 2 θ 1 cot 2 θ = csc 2 θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identitiesMath2org Math Tables Trigonometric Identities sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x)




Pin On Math Videos




Trigonometric Identities Ppt Download
TRIGONOMETRIC IDENTITIES Trigonometric identities are equalities where we would have trigonometric functions and they would be true for every value of the occurring variables Geometrically, these are identities involving certain functions of one or more anglesNotice how a "co (something)" trig ratio is always the reciprocal of some "nonco" ratio You can use this fact to help you keep straight that cosecant goes with sine and secant goes with cosine The following (particularly the first of the three below) are called "Pythagorean" identities sin 2Trigonometric Identities List There are various identities in trigonometry which are used for many trigonometric problems Let us see all the fundamental trigonometric identities here Reciprocal Identities Sin θ = 1/Csc θ or Csc θ = 1/Sin θ;



Www Basd K12 Wi Us Faculty Mbuteyn Trig identities ws Ch 9 key Pdf



Trigonometry Reciprocal Identities Expii
As we know, from trigonometry identities, 1tan 2 A = sec 2 A sec 2 A – 1 = tan 2 A (1/cos 2 A) 1 = tan 2 A Putting the value of cos A = ⅘ (5/4) 2 – 1 = tan 2 A tan 2 A = 9/16 tan A = 3/4There are three basic trigonometric identities in class 10 which relate the trigonometric ratios mutually The three basic trigonometric identities learned in class 10 are Sin 2 A Cos 2 A = 1 Sec 2 A = 1 Tan 2 A Cosec 2 A = 1 Cot 2 A These identities can be derived by considering the right triangle The right triangle is subjected to the Pythagorean theoremTrigonometry Identity tan^2 (x) 1 = sec^2 (x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next in 8



2




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube
The Pythagorean trigonometric identities in trigonometry are derived from the Pythagoras theorem Applying Pythagoras theorem to the rightangled triangle below, we get Opposite 2 Adjacent 2 = Hypotenuse 2 Dividing both sides by Hypotenuse 2Prove the Following Trigonometric Identities `Tan^2 Theta Sin^2 Theta Tan^2 Theta Sin^2 Theta` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 334 Concept Notes &$\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof Take, the theta is an angle of a right triangle, then the tangent and secant are written as $\tan{\theta




Basic Trigonometric Identities And Equations Ppt Download



Http Www Mrsfruge Com Uploads 1 2 0 0 Precalculus Chapter 5 Packet Answers Pdf
Simplify tan^2 x sec^2 Ans 1 Use trig identity 1 tan^2 x = sec^2 x tan^2 x sec^2 x = 1Students are taught about trig identities or trigonometric identities in school and are an important part of higherlevel mathematics So to help you understand and learn all trig identities we have explained here all the concepts of trigonometryAs a student, you would find the trig identity sheet we have provided here useful So you can download and print the identities PDF cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle (See Section 64) tan( − θ) = − tanθ cot( −




Trigonometric Identities
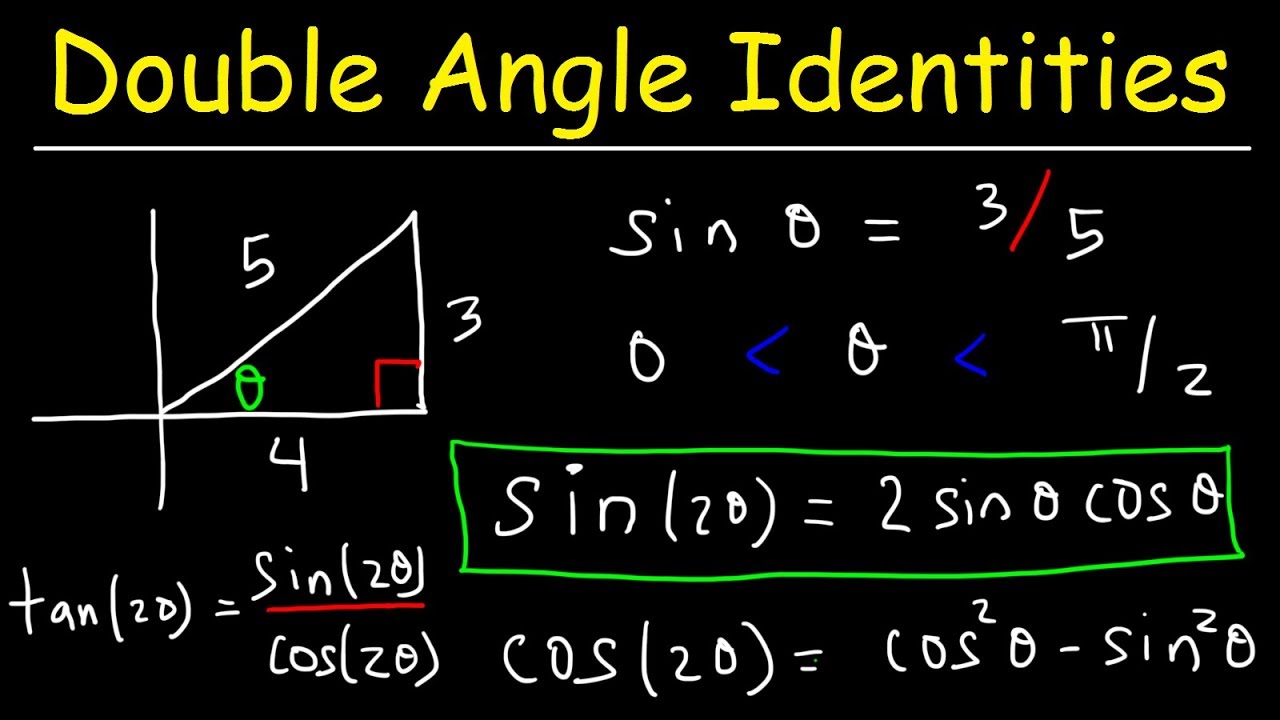



Double Angle Identities Formulas Of Sin Cos Tan Trigonometry Youtube
Periodicity formulas or identities are utilised to shift the angles by \(\frac{\pi }{2},\pi \), and \(2\pi \) The periodicity identities are also termed the cofunction identities All the trigonometric identities are cyclic, which means they repeat themselves after a period The period differs for various trigonometric identitiesTrigonometric identity because it doesn t hold for all values of àä There are some fundamental trigonometric identities which are used to prove further complex identities Here is a list of all basic identities and formulas tan(2 x) = 6 ç Ô á ë ;Trigonometricidentitycalculator Prove tan^{2} x * sin^{2} x = tan^{2} x sin^{2} x en



1




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities tan2 u= 1 cos(2u) 1cos(2u) SumtoProduct Formulas sinusinv= 2sin uCos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more some other identities (you will learn later) include cos x/sin x = cot x 1 tan^2 x = sec^2 x 1 cot^2 x = csc^2 x hope this helped!Trigonometricidentityprovingcalculator prove \tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) en




Exercise Set 4 4 Trigonometric Expressions And Identities Math 1330 Docsity




Ppt Warm Up Powerpoint Presentation Free Download Id
Prove the following trigonometric identities 0 votes 2 views asked 1 hour ago in Trigonometry by Maadesh (7k points) Prove the following trigonometric identities tan 2 Asec 2 B Sec 2 Atan 2 B = tan 2 A tan 2 B trigonometric identitiesAnswer As below (1 tan^2 theta) / (1 tan^2 theta)# sankarankalyanam 1 How do you use a double angle identityBasic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian plane
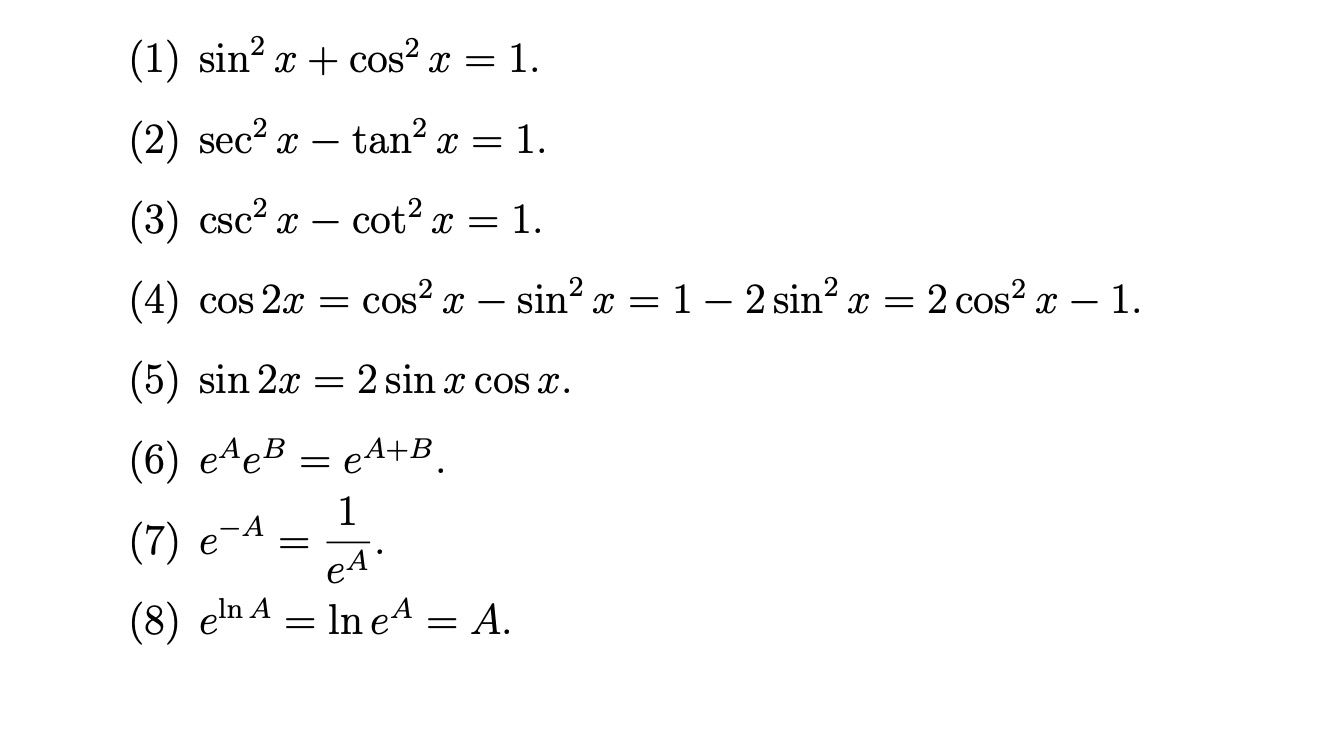



Here Is A List Of Identities Involving Trigonometric Chegg Com




Trig Identities Turn The Wheel
Trigonometric Identities 43 Introduction A trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles) There are a very large number of such identities In this Section we discuss only the most important and widely used Any engineer using trigonometry in an applicationTrigonometry Trigonometric Identities and Equations Double Angle Identities Key Questions How do you use double angle identities to solve equations?Definitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse The six trigonometric functions are defined for every real number, except, for some of them




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
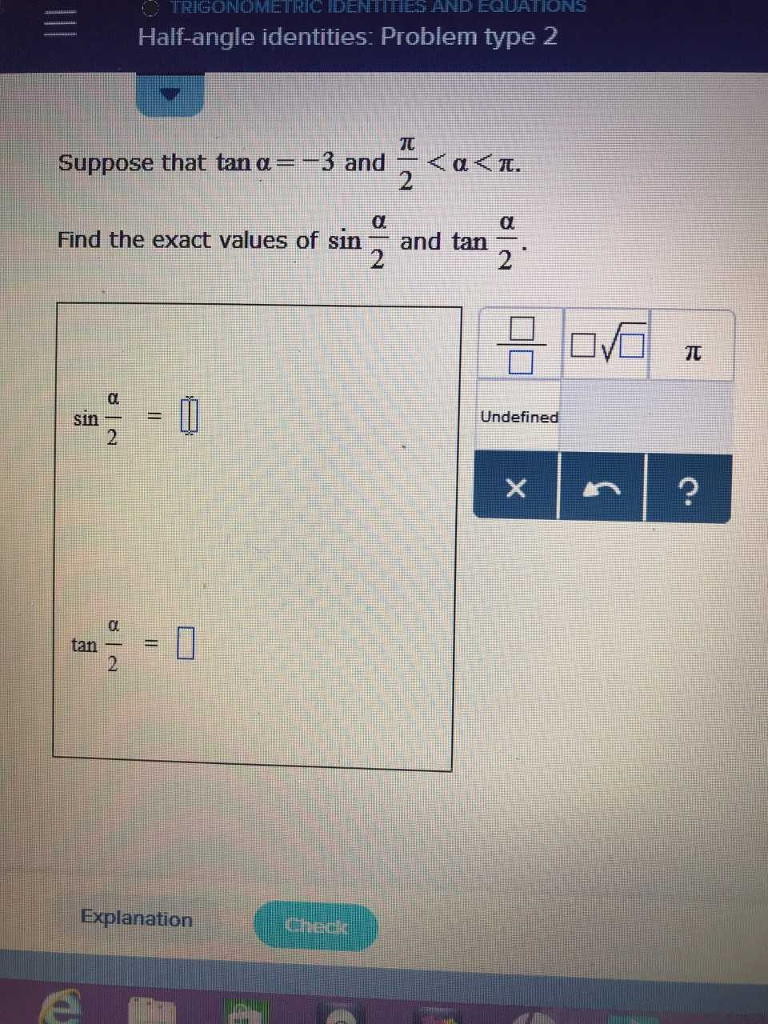



Trigonometric Identihes And Equationss Half Angle Chegg Com
Conditional trigonometrical identities We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identitiesThis is a list of the basic trigonometric identities You may want to work through a tutorial, with examples and detailed solutions, on Using Trigonometric Identities Review of Trigonometric Identities Pythagoren Identities sin 2 x cos 2 x = 1 tan 2 x 1 = sec 2 x 1 cot 2 x = csc 2 x Reciprocal Identities csc x = 1 / sin x sec x = 1 / cos x⋯ csc =5 8 A ?




Quiz Worksheet Trigonometric Identities Unit Circles Study Com




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Find All Solutions Of The Following Equations Between Chegg Com




Grade 12 Trigonometry Sum Or Difference Identity Homeworkhelp



Http Www Math Miami Edu Dscheib Teaching Fall09 Mac1147 Lecture Notes Files Section 7 2 Notes Pdf




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




Solved I Solve The Following Using Fundamental Trigonome Chegg Com




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
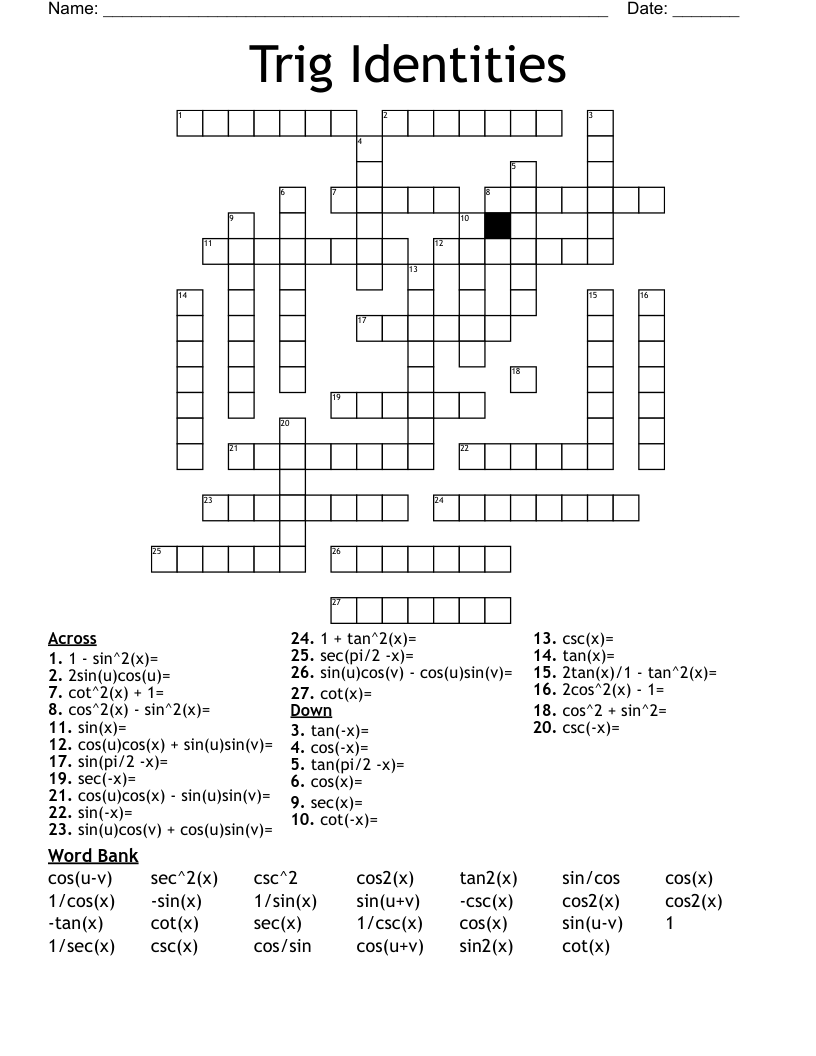



Trig Identities Crossword Wordmint




Trigonometric Identities Trigonometric Functions Trigonometry



3




Integration Using Trigonometric Identities 2 Examsolutions Youtube



Www Brockport Edu Academics Tutoring Docs Trigonometric Identities Pdf



2




Trigonometry Laws And Identities Tool Eeweb Community
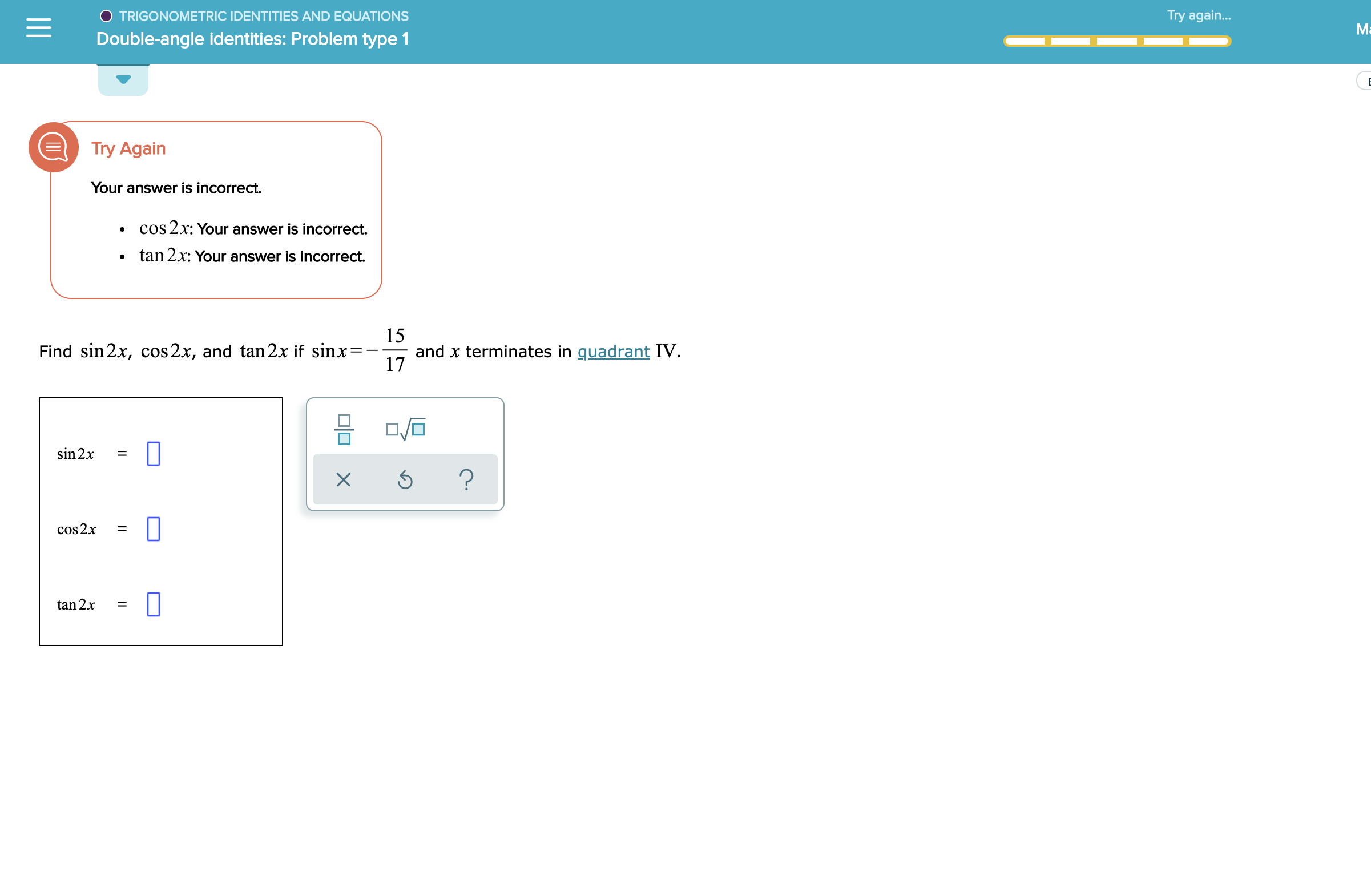



Answered O Trigonometric Identities And Bartleby



Www Nhvweb Net Vhs Math Jfranz Files 17 08 5 1 2 16 Even Solutions Pdf




Samantha Douglas Precal 30 Trigonometric Identities Practice Test Answers




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Trigonometric Identity Examples Solutions Videos




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
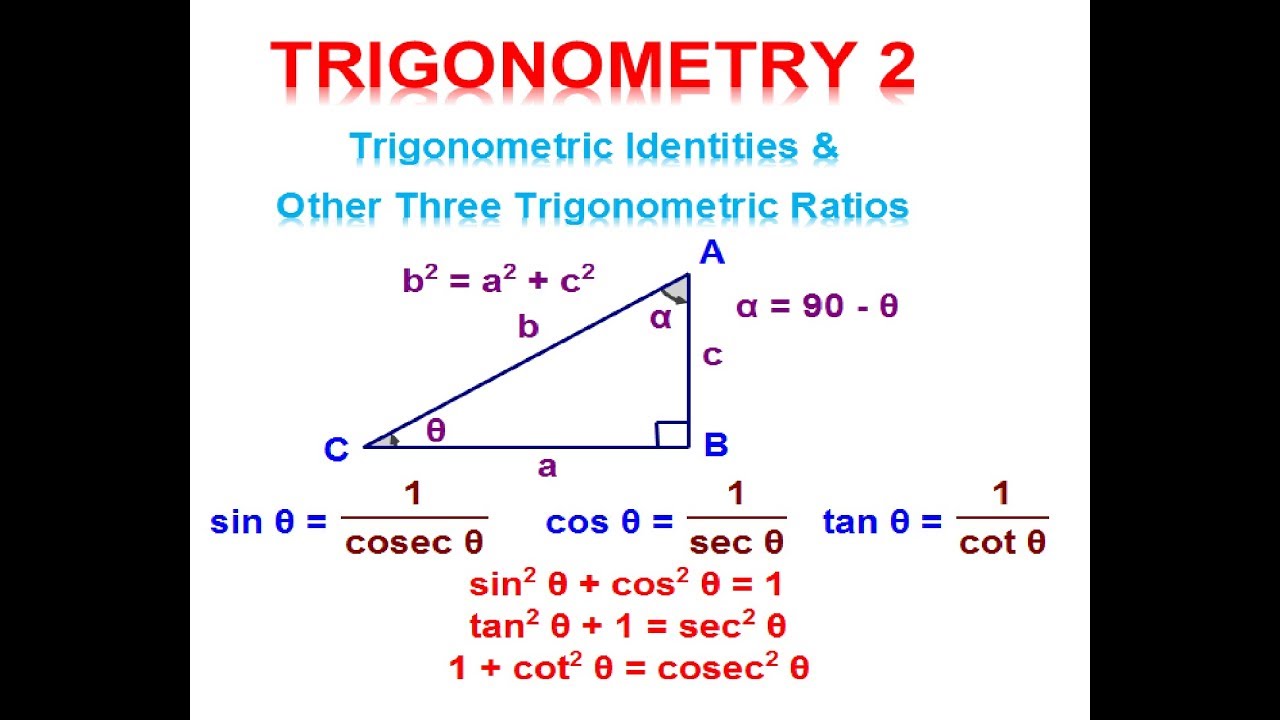



W H A T I S A T R I G O N O M E T R I C I D E N T I T Y Zonealarm Results




Which Of The Following Are Trigonometric Identitie Gauthmath




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



Http Faculty Atu Edu Mfinan 13 Lecture18 Pdf



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf



Www3 Nd Edu Nancy Math Info Trigformulas Pdf



Lsamathwilson Weebly Com Uploads 2 2 5 4 Pc 5 2 Verifying Trigonometric Identities Solutions Pdf




Trigonometric Equations And Identities Trigonometry Math Khan Academy



3



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download



Schoolwires Henry K12 Ga Us Cms Lib Ga Centricity Domain 1610 Unit 4 test trig identities a Pdf




Prove The Following Trigonometric Identities Show Gauthmath




Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube




Power Reducing Formulas And How To Use Them With Examples Owlcation



Http Www Whsd K12 Pa Us Userfiles 1598 Classes 9713 Trig chapter 5 notes Pdf



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf




Trig Identities All List Of Trigonometric Identities Learn Trigonometry




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Double Angles Identity Is Part Of Trigonometry Identity




Double Angle Formulas What Are Double Angle Formulas Examples
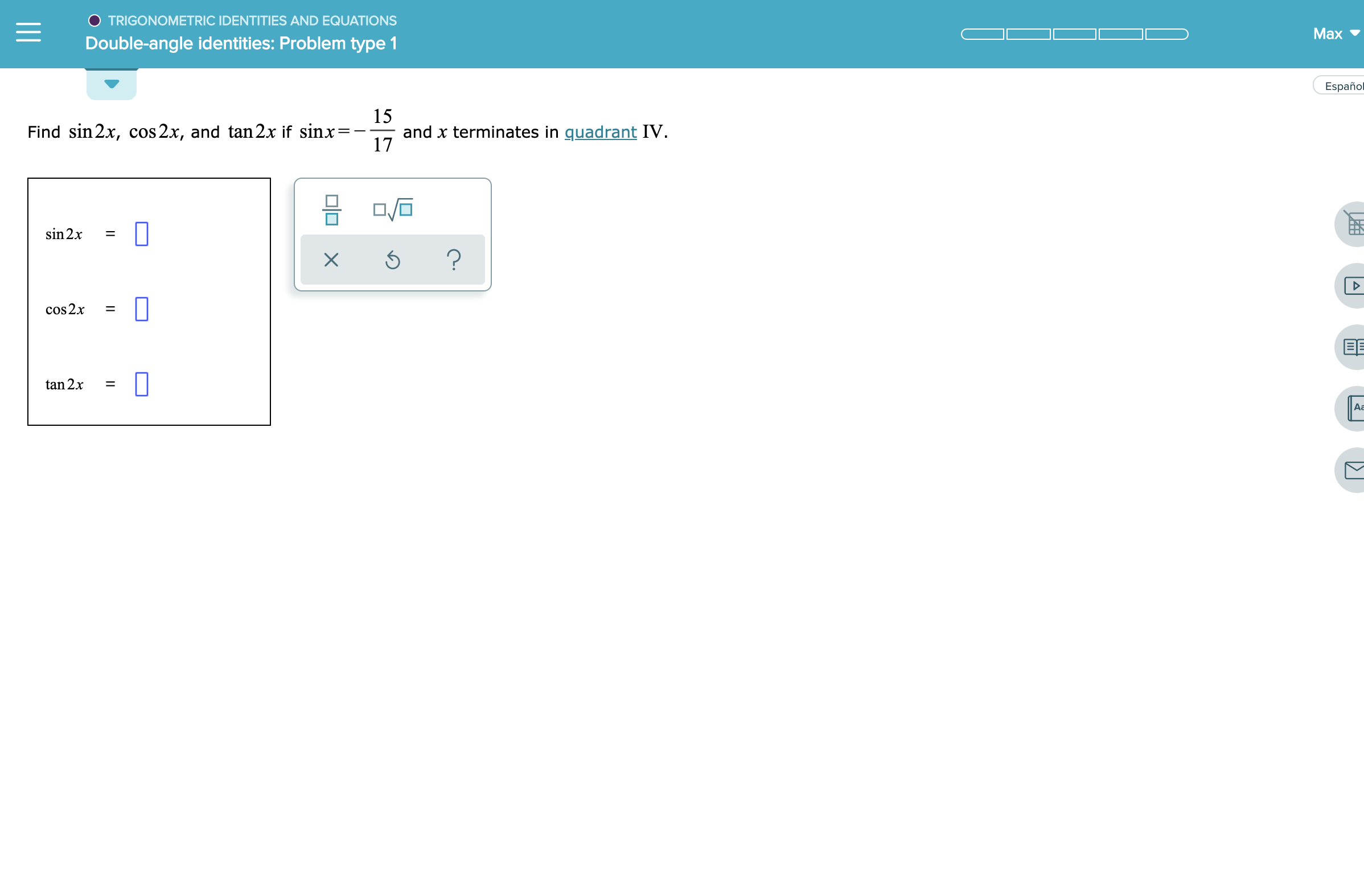



Answered O Trigonometric Identities And Bartleby




10 4 Trigonometric Identities Pdf Free Download
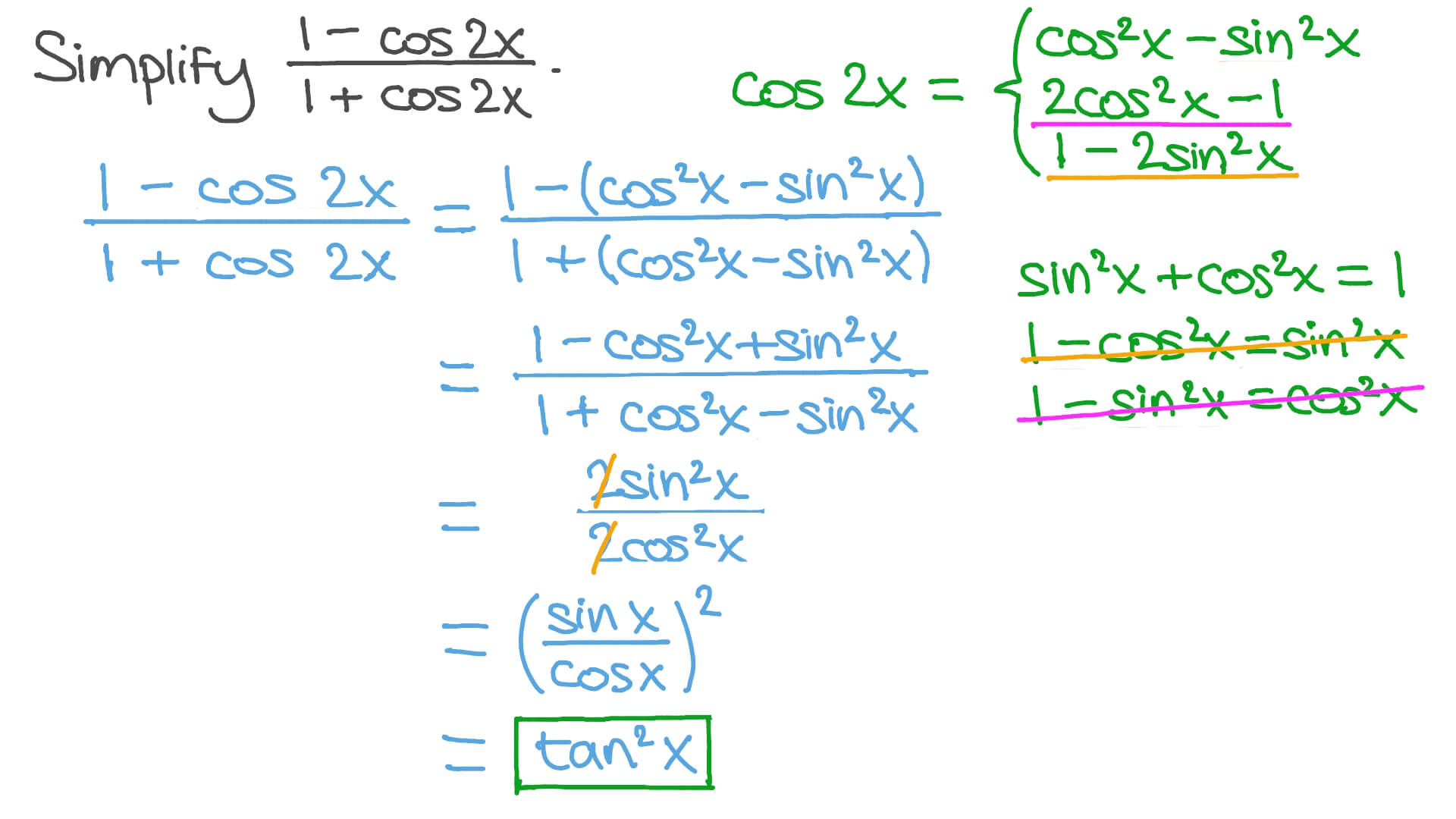



Question Video Simplifying Trigonometric Expressions Using Double Angle Identities Nagwa




Cofunction Identities In Trigonometry With Proof And Examples Owlcation
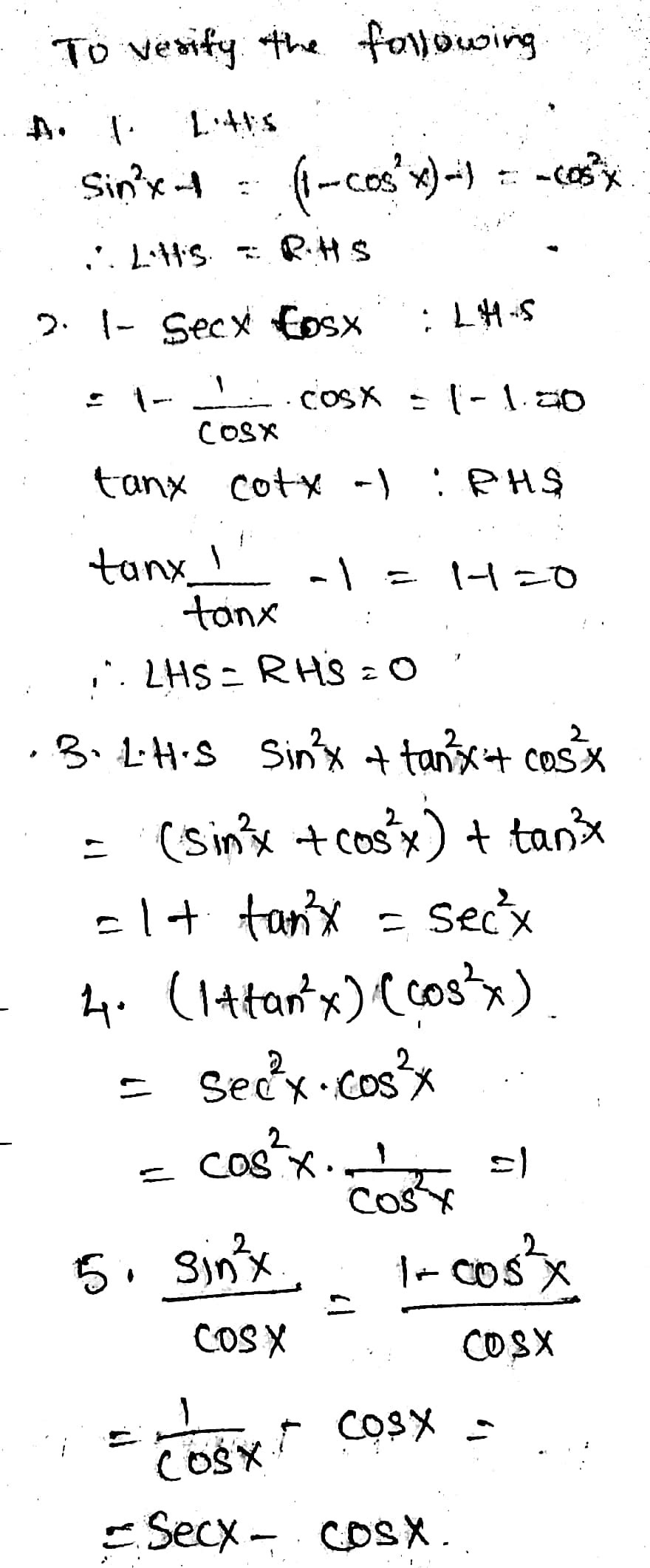



Directions Verify The Following Trigonometric Id Gauthmath




Lesson 5 2 Verifying Trigonometric Identities Trig Ridge Style




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



Www Jmap Org Worksheets F Tf C 8 Provingtrigonometricidentities Pdf




32 Trig Identities




Trigonometric Identities




Trigonometric Identities Solutions Examples Videos




Cos Sin Tan Csc Sec Cot



Solved Find The Remaining Five Trigonometric Functions Of 0 See Example 1 Sin A 0 In Quadrant Ii 32 Cos 0 0 In Quadrant I 33 Tan 0 Course Hero




List Of Trigonometric Identities Wikipedia




Trigonometric Identities




Trigonometric Identity Examples Solutions Videos




Verify The Trigonometric Identity 1 1 Sin 2 X 1 Tan 2 X In 21 Identity Sins Math




Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity




Tan 2x Formula What Is Tan 2x Formula Examples




List Of Trigonometric Identities 2 Docx Document




Double Angle Identities Formulas Of Sin Cos Tan Trigonometry Youtube




Trig Identities Study Sheet



Mi Schoolwires Net Cms Lib Mi Centricity Domain 433 Trig identities notes and hw packet march 18 Pdf



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




Trigonometric Identities Cheat Sheet
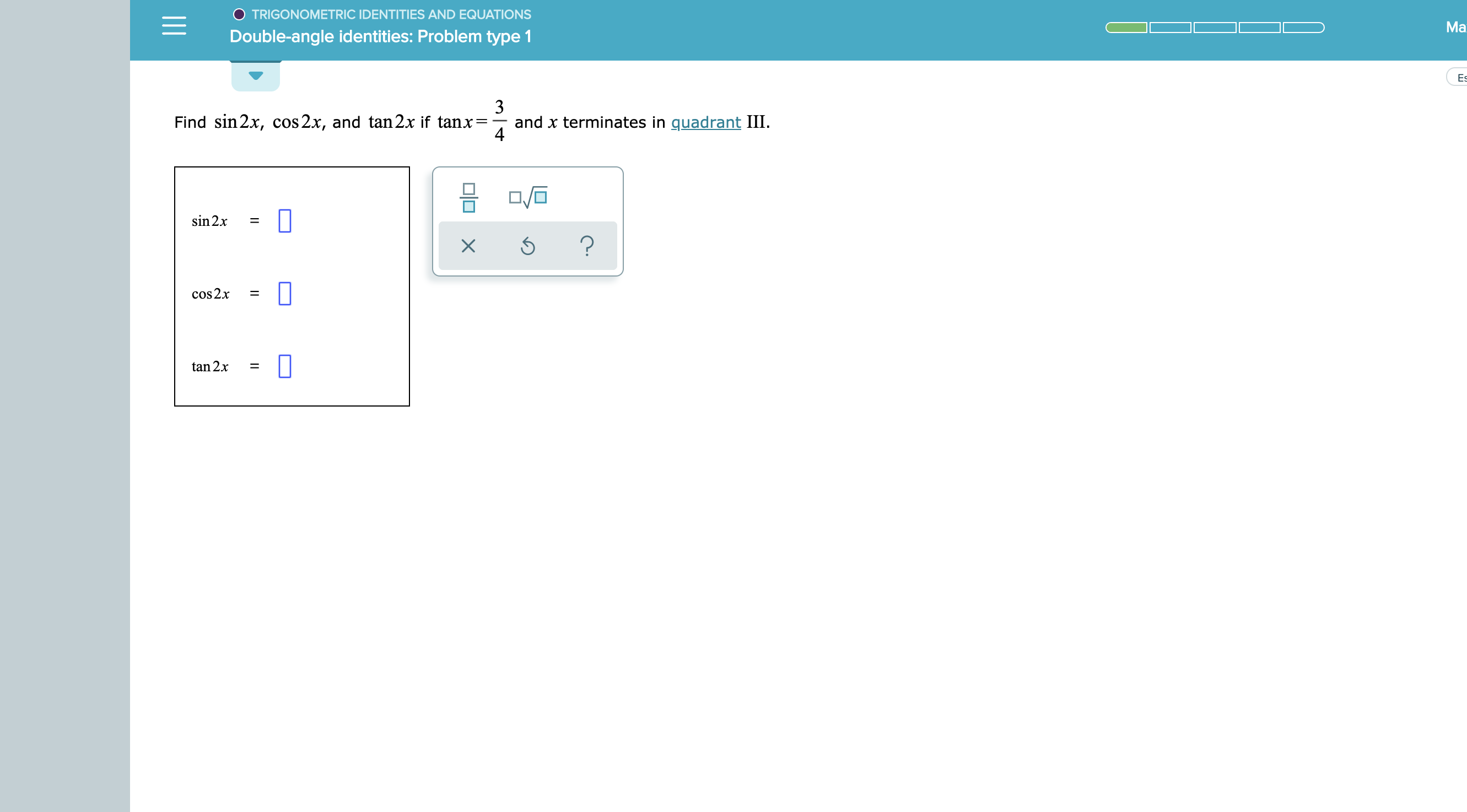



Answered O Trigonometric Identities And Bartleby



Http Scibug Com Public Docs Trigonometry Cheat Sheet Pdf



Common Identities Properties Of Trigonometric Functions 4 8 Sideway Output To
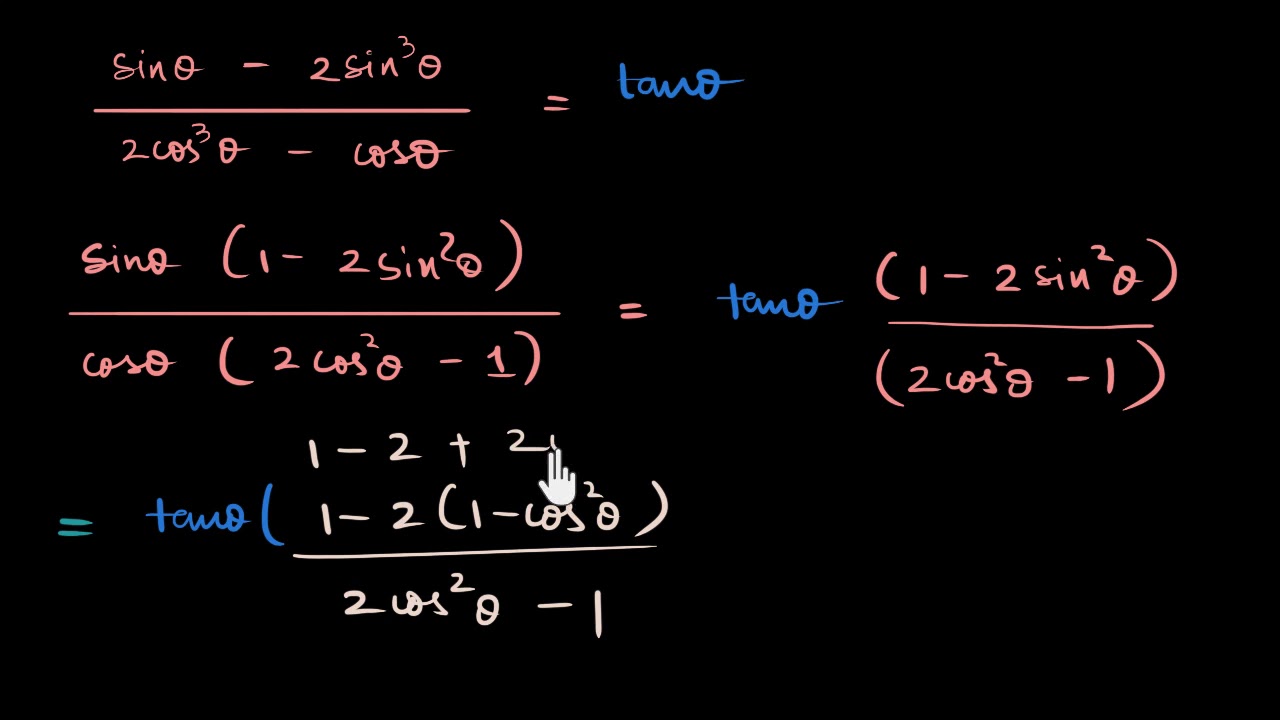



Trigonometric Identity Example Proof Involving Sin Cos And Tan Video Khan Academy



Mrsmkramer Weebly Com Uploads 3 5 9 0 Trig Cheat Sheet Pdf




5 1 5 2 Trigonometric Identities Ppt Download




Trigonometric Identities Docsity




Trigonometry Identities And Equations Ppt Download




Prove The Trigonometric Identity Tan 2 Theta 1 Cos 2 Theta 1 Maths Introduction To Trigonometry Meritnation Com




Trigonometric Identities A Plus Topper




Powers Of Trigonometric Functions



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf




Double Angle Identities Joke Worksheet Math Love



0 件のコメント:
コメントを投稿